ErKang

Java后端

发表于 更新于

什么是布隆过滤器?

布隆过滤器是一种数据结构，用于快速判断一个元素是否存在于一个集合中。

使用场景

✨初始使用：注册用户时就向容器中新增数据，就不需要任务向容器存储数据了。
✨使用过程中引入：读取数据源将目标数据刷到布隆过滤器。

缺点

可能存在一定的误判。
阅读全文 »

发表于 更新于

读写锁是什么？

读写锁（Read-Write Lock）是一种同步机制，用于解决多线程环境下的资源访问问题。它允许多个线程同时读取共享资源，但在写入资源时，只有一个线程可以进行写操作，并且在写操作进行期间，不允许其他线程读取该资源。读写锁的设计目的是提高系统在多线程环境下的并发性，同时确保数据的一致性。
阅读全文 »

发表于

COALESCE函数

作用：处理空值（NULL值）,返回其参数中第一个非空的值

1
COALESCE(s.today_pv, 0) AS todayPv,

LEFT JOIN

作用：是SQL中的一种连接操作。它会返回左表（即连接中写在LEFT JOIN前面的那个表）的所有记录，以及右表中与左表匹配的记录。如果右表中没有与左表匹配的记录，结果中相应右表的字段将显示为NULL。

1
...FROM t_link t LEFT JOIN t_link_stats_today s...

ON

作用：连接条件

1
ON t.gid = s.gid AND t.full_short_url = s.full_short_url AND s.date = CURDATE()

WHERE

作用：过滤条件

1
WHERE t.gid = #{gid} AND t.enable_status = 0 AND t.del_flag = 0

#{gid}

作用：表示一个参数化的值，在实际执行查询时会被替换为具体的值

1
WHERE t.gid = #{gid} AND t.enable_status = 0 AND t.del_flag = 0

发表于

1.新建数据库表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
CREATE TABLE `t_link_stats_today` (
  `id` bigint(20) NOT NULL AUTO_INCREMENT COMMENT 'ID',
  `gid` varchar(32) DEFAULT 'default' COMMENT '分组标识',
  `full_short_url` varchar(128) DEFAULT NULL COMMENT '短链接',
  `date` date DEFAULT NULL COMMENT '日期',
  `today_pv` int(11) DEFAULT '0' COMMENT '今日PV',
  `today_uv` int(11) DEFAULT '0' COMMENT '今日UV',
  `today_uip` int(11) DEFAULT '0' COMMENT '今日IP数',
  `create_time` datetime DEFAULT NULL COMMENT '创建时间',
  `update_time` datetime DEFAULT NULL COMMENT '修改时间',
  `del_flag` tinyint(1) DEFAULT NULL COMMENT '删除标识 0：未删除 1：已删除',
  PRIMARY KEY (`id`),
  UNIQUE KEY `idx_unique_full-short-url` (`full_short_url`) USING BTREE
) ENGINE=InnoDB AUTO_INCREMENT=2 DEFAULT CHARSET=utf8mb4;
阅读全文 »

发表于 更新于

字节码文件组成部分：
魔数-标识文件类型的文件头，固定为0xCAFEBABE
主、副版本号-(1.2版本后，大版本号计算格式：主版本号-44)
常量池、符号引用【面试题：int i=0，i=i++,i还是为0】
方法

字节码指令：
iconst
istore
iload
iadd
return
iinc…by…

阅读全文 »

发表于 更新于

占坑

发表于 更新于

一、先在Terminal里面分别输入两行命令行

1
2
ip addr show
nmcli device status

然后就可以看到当前Linux系统的ip地址和网卡配置情况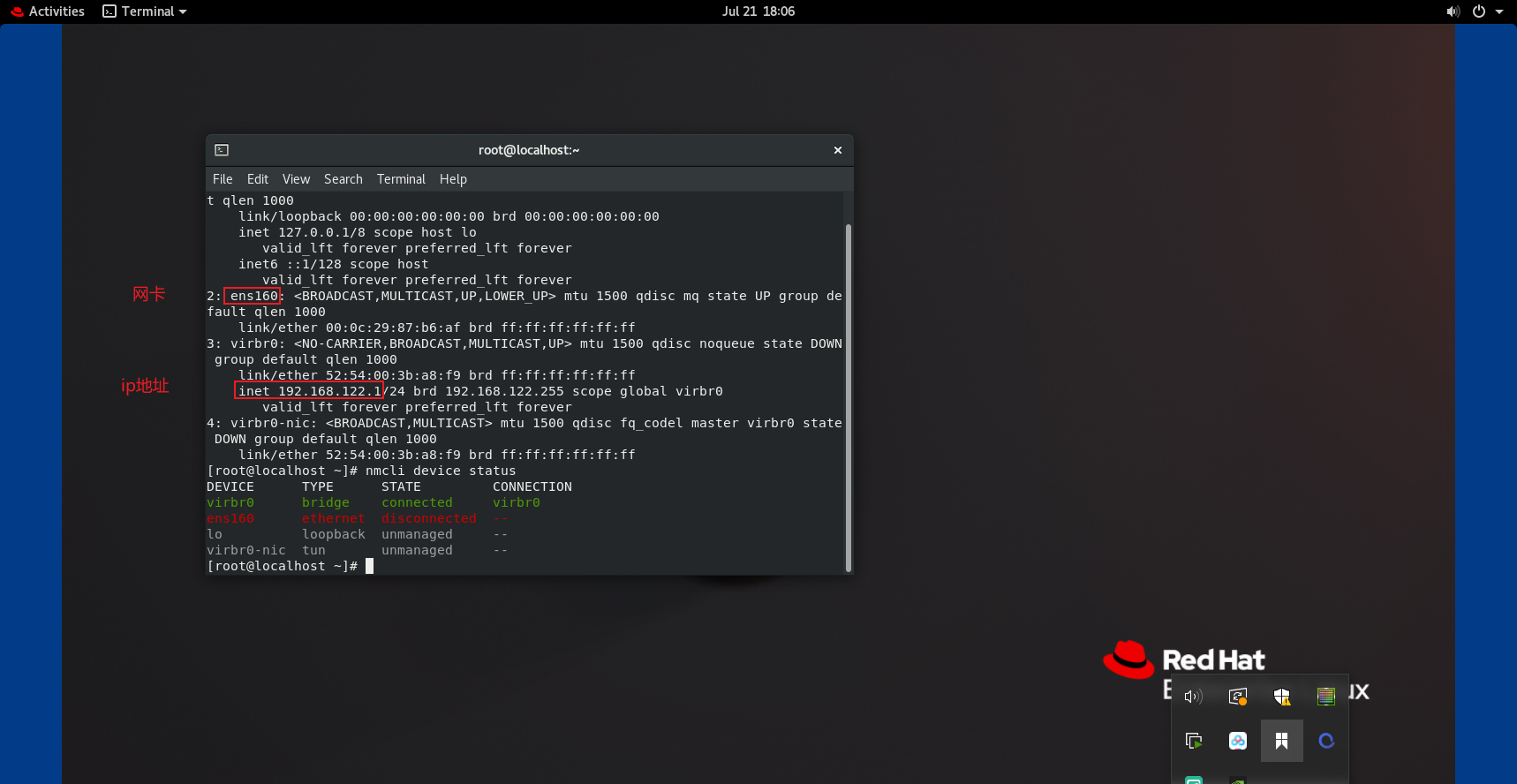
1.png
可以看到，ens160网卡的状态显示为disconnected，也就是当前系统是处于无法联网的状态

阅读全文 »

发表于 更新于

网络图片
Linux

图床
银帆公园

歌单上传

单曲分享

本地图片
个人微信

链接
Baidu

视频

代码块测试

1
这是一行文字

发表于 更新于

编程题

  1. 输入三个整数作为三角形的三条边，判断如果不能构成一个三角形，则输出“not a triangle”;否则如能构成一个直角三角形，则输出”yes”;否则输出”no”。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    #include <stdio.h>

    int main()
    {
    	int a, b, c;
    	while(scanf("%d %d %d",&a, &b,&c)!=EOF)  //实现多组数据重复输入
    	if((a+b>c)&&(a+c>b)&&(b+c>a))  //判断是否构成三角形
    		{
    			//判断是否构成直角三角形
    			if((a*a + b*b == c*c)||(a*a + c*c == b*b)||(b*b + c*c == a*a))
    			printf("yes\n");
    			else printf("no\n");
    		}
    	else printf("not a triangle\n");
    	
    	
    	return 0;
    }

    复习：C 库函数 - scanf()

    阅读全文 »

发表于 更新于

本文转载自知乎用户 瞻望重逢 的文章《质数的孤独》
以下为正文

质数只能被一和它自身整除。在自然无穷序列中，它们处于自己的位置上，和其他所有数字一样，被前后两个数字挤着，但它们彼此间的距离却比其它数字更远一步。它们是多疑而又孤独的数字。……在质数中还有一些“孪生质数”，它们是离得很近的一对质数，几乎是彼此相邻。在它们之间只有一个偶数，阻隔了它们真正的亲密接触，11 和 13,17和19,41和43，假如你有耐心数下去，你会发现这样的孪生质数会越来越难以遇到，越来越常遇到的是那些孤独的质数，它们迷失在那个纯粹由数字组成的寂静而又富于节奏的空间中。此时，你会不安地预感到，到那里为止，那些孪生质数的出现只是一种偶然，而孤独才注定是它们真正的宿命。然后，当你准备放弃的时候，却又能遇到一对彼此仅仅相邻的孪生质数。因此，数学家们有一个共同的信念，那就是要尽可能地数下去，早晚会遇到一对孪生质数，虽然没人知道它们会在哪里出现，但迟早会被发现。

2760889966649
2760889966651

阅读全文 »
0%